PRIMENA STATIČKOG PENETRACIONOG OPITA (CPT). U okvirima metoda koje primenjuje mehanika tla, granična nosivost baze šipa može se proceniti primenom rezultata ispitivanja tla statičkim penetrometrom koji, osim otpornosti vrha daje i rezultate merenja bočnog trenja, direktnim preslikavanjem napona sa penetrometra na šip. Statički penetrometar se, pre svega koristi za ispitivanje peskova. Granična nosivost baze šipa je proporcionalna otporu vrha penetrometra:
|
qb,f |
= |
αbqc |
(9.95) |
Koeficijent αb je korektivni koeficijent koji zavisi od načina ugrađivanja šipa u tlo. Za pobijene ili utisnute šipove može se uzeti da je granična nosivost baze šipa jednaka otporu vrha statičkog penetrometra tako da je αb=1,0, s obzirom da statički penetrometar predstavlja minijaturni utisnuti šip. Za bušene šipove se orijentaciono može usvojiti da je αb≈1/2, a ovaj koeficijent se može korigovati rezultatima probnih opterećenja i lokalnim iskustvima tako da može biti i manji, do αb≈1/3.

S obzirom na moguću varijabilnost penetracionog otpora i razlike dimenzija penetrometra i šipa, za računsku veličinu otpora vrha statičkog penetrometra jedna od mogućmosti je da se usvaja srednja vrednost otpora vrha na potezu dužine 4 prečnika šipa, i to 1 (jedan) prečnik ispod baze i 3 (tri) prečnika iznad baze šipa, iako ima i drugačijih predloga. Na ovaj način se, bar kvalitativno, imaju u vidu mehanizmi loma tla prikazani na Slici 9.16.
Za procenu smičućeg otpora po omotaču šipa koriste se razne empirijske korelacije sa otporom vrha penetrometra, (na primer, Bustamante i Gianeselli 1981), iako se mehanizam proloma tla pod vrhom penetrometra u velikoj meri razlikuje od oblika interakcije omotača šipa i okolnog tla. Na primer, De Beer (1985) predlaže konzervativnu korelaciju u obliku:
τs,f = qc/200 ako je qc ≥ 20 MPa odnosno τs,f = qc/150 ako je qc ≤ 10 MPa pri čemu je gornja granica smičućeg otpora po omotaču šipa 100-120 kPa.
Alternativno, Fleming i dr. (1985), na osnovu analize rezultata probnih opterećenja sugerišu da je vrednost Ks u formuli (9,86) približno N*q /50, a da je δ = φ/cv, jer se dilatancija ne odvija u kontaktu sa šipom. Ako se usvoji daje N*q = qc/σ/v dobij a se da je τs,f = (qc/50) tan φ/cv. Ovo ukazuje daje za omotač šipa u tipičnom kvarcnom pesku smičući otpor τs,f ≥ qc/100 ili oko 1% otpora vrha penetrometra, red veličine koji se može naći u nekoliko stranih normativa i radovima istraživača.
Opit statičke penetracije treba uvek predvideti programom geotehničkih istražnih radova ukoliko se ocenjuje da će se temeljenje izvesti na šipovima u krupnozrnom tlu, jer postoji relativno bliska analogija u ponašanju šipa i statičkog penetrometra.
PRIMENA STANDARDNOG PENETRACIONOG OPITA (SPT). Rezultati standardnog penetracionog opita se mogu upotrebiti za prognozu granične nosivosti baze šipa, u načelu, na tri načina.
Prvi način podrazumeva da se na osnovu empirijskih korelacija procene parametri smičuće čvrstoće i deformabilnosti (ako to teorijska metoda zahteva), koji se zatim uvrste u ranije date teorijske izraze koji te parametre sadrže.
Drugi način bi podrazumevao primenu korelacije između broja udara u standardnom penetracionom opitu sa otporom vrha statičkog penetrometra (Slika 7.32) te primenu ranije opisanog postupka korišćenjem CPT opita.
Treći način bi bio direktno empirijski, pri čemu se obično koristi oblik:
|
qb,f |
= |
K N |
(9.96) |
gde je:
K koeficijent koji zavisi od vrste tla i načina ugrađivanja šipa (MN/m2),
N broj udara u standardnom penetracionom opitu (SPT).
Orijentacione vrednosti koeficijenta K se kreću u sledećim granicama:
| Pobijen šip | Bušeni šip | |
| Pesak | 0,40 - 0,45 | ~0,10 |
| Prašina | 0,20 - 0,35 | ~0,12 |
| Glina | 0,12 - 0,20 | ~0,15 |
Gore dati empirijski koeficijenti ukazuju da baze bušenih šipova u krupnozrnom tlu imaju znatno manju graničnu nosivost od pobijenih sa istim dimenzijama.
PROBNO OPTEREĆENJE ŠIPA. S obzirom na složenost problema nosivosti šipova i neveliku pouzdanost teorijskih rešenja zbog varijabilnosti parametara koji u formulama figurišu, pre svega veličina Ks i φ, zbog osetljivosti faktora nosivosti Nq na veličinu ugla φ u peskovima, i veličine α u glinama, razlika između proračunom prognoziranih veličina i stvarnih nosivosti može iznositi i preko 50%. Zbog toga, kada se ne raspolaže pouzdanim rezultatima ranije izvršenih ispitivanja u sličnim lokalnim geotehničkim uslovima, pri izgradnji većih objekata je preporučljiva primena probnih opterećenja. U zemljama sa dobro proučenim geotehničkim uslovima i intenzivnom gradnjom u prošlosti i sa velikim fondom sistematizovanih rezultata ispitivanja izvršenih za potrebe građenja objekata, naročito CPT opita, probna opterećenja se relativno retko provode. Sa druge strane, u nekim zemljama se primena probnih opterećenja zahteva, obavezna je u određenim okolnostima, a način izvođenja često je propisan tehničkom regulativom.
U načelu, najčešće se rade probna opterećenja pojedinačnog šipa vertikalnom silom pritiska. Ređe se primenjuju probna opterećenja silom zatezanja ukoliko će šipovi biti opterećeni takvom silom ili radi izdvajanja komponente nosivosti omotača stabla od ukupne nosivosti, jer se tako eliminiše komponenta nosivosti baze šipa. Ukoliko će šipovi biti opterećeni i većom horizontalnom silom, mogu se izvesti i takva probna opterećenja, ali se ovaj problem ovde neće obrađivati.
Za obezbeđenje reakcije za aktivno vertikalno opterećenje šipa mogu se primenjivati različite dispozicije opita, od kojih su neke prikazane na Slici 9.20. Najjednostavniji, ali ne uvek i najekonomičniji opit podrazumeva balast, kao što je to prikazano na Slici 9.20-a. Balast mora biti dovoljne težine kako bi se suprotstavio reaktivnom opterećenju hidrauličke prese kojom se opterećuje vrh šipa. Obično se preporučuje da balast bude za 10-20% teži od planirane maksimalne sile probnog opterećenja. Oslanjanje balasta treba izvesti što dalje od probnog šipa, kako bi se minimizirao uticaj balasta na šip. Ovo odstojanje ne treba da bude manje od 2 m za šipove uobičajenih dimenzija. Sa teorijske tačke gledišta, ispravnije bi bilo direktno opterećivati šip balastom bez primene hidrauličke prese i oslonaca za balast, jer se time eliminiše uticaj promene reakcija balasta na sleganje, ali je takva dispozicija opita retko kad praktično izvodljiva. Osim primene balasta, reakcije se mogu obezbediti sidrenjem krutog čeličnog nosača za susedne šipove koji će reaktivnim opterećenjem biti opterećeni čupanjem (Slika 9.20-b), ili sidrenjem privremene naglavnice šipa u slojeve čvršćeg tla ili stene na pristupačnoj dubini (Slika 9.20-c).
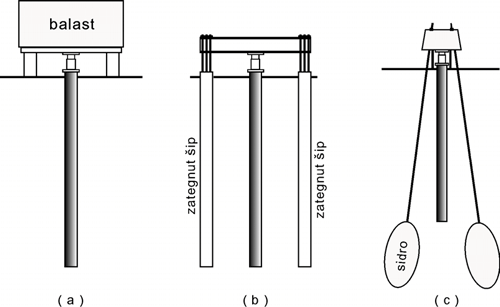
Slika 9.20. Dispozicije probnih opterećenja šipa vertikalnom silom pritiska.
U načelu, poželjno je provesti probno opterećenje šipa do loma tla (ili šipa) jer se tako dobija granična nosivost, što omogućuje izbor dopuštenog opterećenja sa racionalnim faktorom sigurnosti. To zahteva relativno veliki balast, probni šip se obično ne može više upotrebiti u nošenju konstrukcije ili se posebnom analizom mora dokazivati da su uticaj i istorije prethodnog opterećivanja na njegovo buduće ponašanje u temeljima konstrukcije obuhvaćeni na odgovarajući način. Zbog toge se, radi smanjenja troškova, šip može opterećivati do veličine koja je za 1,5 do 2,0 puta veće od njegovog opterećenja procenjenog proračunom na osnovu podataka o tlu, što može biti i manje od sile koja izaziva lom tla.
Probno opterećenje se postepeno povećava, kontinulano ili u stepenastim priraštajima, i pri tome registruje sleganje gornjeg kraja, vrha šipa. Veličinu priraštaja opterećenja treba prilagoditi metodi koja će se upotrebiti pri interpretaciji rezultata merenja. Ukoliko se upotrebi ovde prikazan postupak, koji podrazumeva intervalsku hiperboličku zavisnost između sile i sleganja, opterećivanje treba provesti u desetak priraštaja jednake veličine do maksimalnog opterećenja, bez rasterećivanja tokom opita, osim, naravno, rasterećivanja nakon dostignutog maksimalnog opterećenja u opitu. Lom se ogleda u relativno brzom sleganju pri konstantnom ili sporom opterećivanju. Šip "tone", Slika 9.21. Takva definicija graničnog opterećenja nije dovoljno precizna, naročito ako se ima u vidu da se obično događa lokalni ili probojni lom bez naglašene ili jasne vrednosti maksimuma.
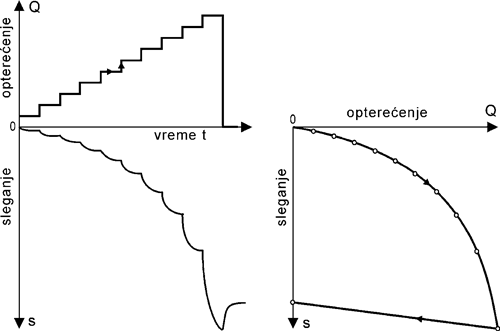
Slika 9.21. Probno opterećivanje šipa – dijagrami.
U propisima raznih zemalja i radovima istraživača se mogu naći mnoge definicije loma tla pri probnom opterećenju šipa. Neki kriterijumi loma mogu biti toliko arbitrarni da rezultat zavisi od razmere koordinatnih osa upotrebljenih za prikazivanje opterećenja i sleganja, ili čak i od subjektivnog mišljenja obrađivača rezultata. Neke definicije loma za granično opterećenje proglašavaju silu koja utisne šip za veličinu koja je jednaka nekom procentu prečnika šipa (2,5%, 5% ili 10%). Da bi kriterij loma imao racionalnu osnovu, on se mora zasnivati na nekom matematičkom pravilu koje daje konzistentne rezultate, ne zavisi od razmere grafika i ne zavisi od subjektivnog stava obrađivača. Pri tome je veoma poželjno da analitička zavisnost između sile i sleganja bude takva da omogućava pouzdanu ekstrapolaciju rezultata ispitivanja ukoliko je šip tokom probnog opterećenja bio izložen maksimalnoj sili koja je očigledno manja od granične vrednosti. Ovde će se navesti jedna metoda koja takve uslove zadovoljava.
Metoda hiperboličke ekstrapolacije se pripisuje nekolicini istraživača koji su, izgleda, ovaj postupak za određivanje granične nosivosti šipa predložili sasvim nezavisno jedan od drugog, ali svi polaze od predloga koji je za aproksimaciju naponsko-deformacione krive u opitu triaksijalne kompresije predložio Kondner (1963). Za sleganja s > s1, koja su u području većih opterećenja i većih merenih sleganja, (Slika 9.22), opterećenje Q u funkciji sleganja s se aproksimira hiperbolom u obliku:
|
Q |
= |
s |
(9.97) |
|
a + b s |
gde su a i b parametri prave transformisane hiperbole koji se mogu odrediti iz merenih veličina sleganja nakon ispisivanja gornjeg izraza u obliku
|
s |
= |
a + bs |
(9.98) |
|
Q |
Kada sleganje s teži beskonačnosti, asimptotska vredost izraza (9.97) daje jednu moguću definiciju granične nosivosti šipa kao:
|
Qf |
= |
1 |
(9.99) |
|
b |
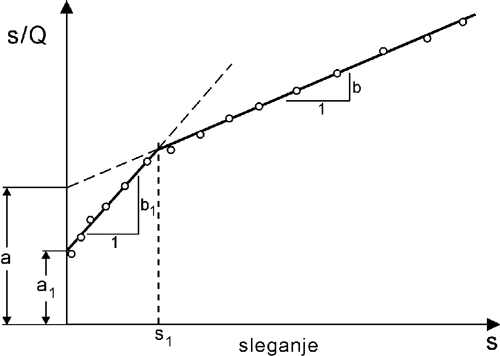
Slika 9.22. Hiperbolička funkcija za određivanje granične nosivosti šipa
Poređenja na konkretnim primerima sa raznim drugim metodama bi pokazala da metoda hiperboličke ekstrapolacije daje gornju granicu vrednosti granične sile, jer definiše asimptotsku veličinu sile za beskonačnu veličinu sleganja, sa razlikom koja se kreće između 10% i 20%. Kako zavisnost između opterećenja i sleganja pri lokalnom ili probojnom lomu tla, sa fizičke tačke gledišta nema asimptotu, već sila raste, istina sasvim blago sa povećanjem sleganja, modifikacija ovog postupka proističe iz primene ranije navedenog praktičnog stava o odnosu sleganja pri lomu i prečnika šipa. Ako se usvoji daje granična sila pri lomu tla veličina opterećenja koja izaziva sleganje od 10% prečnika šipa B, dobija se daje, sa istim parametrima a i b, granično opterećenje šipa:
|
Qf |
= |
0,1 B |
(9.100) |
|
a + 0,1b B |
Ovaj izraz daje vrednosti koje su za 10% do 20% manje od jasno definisane asimptotske vrednosti i veličina granične sile je slična rezultatima drugih metoda ali nema njihove slabosti o kojima je bilo reči. Na ovaj način se granična nosivost šipa definiše kao veličina opterećenja koja u hiperboličkom opisu daje veličinu sleganja od 10% prečnika šipa, podrazumevajući pri tome da to može biti i ekstrapolisana vrednost ukoliko probno opterećenje nije provedeno do ove veličine sleganja.
Konvencionalnim opitima probnog opterećenja, sa opisanom interpretacijom ispitivanja, dobija se samo ukupno granično opterećenje, pri čemu je to zbir komponenti nosivosti baze šipa i omotača. Moguće je iz oblika krive proceniti pojedinačni doprinos ovih komponenti ukupnoj nosivosti, što se po nekad u praksi i čini, pri čemu se imaju u vidu rezultati ispitivanja posebno instrumentiranih šipova kojima su ovi doprinosi merenjima ustanovljeni. Generalno je ustanovljeno da su relativno mala sleganja šipa dovoljna da se u punoj meri mobilišu smičući naponi i granična nosivost omotača šipa. Za dostizanje granične nosivosti baze šipa potrebna su znatno veća pomeranja, kao što je to ilustrovano na Slici 9.15.
U okviru hiperboličkog opisa zavisnosti sleganja od opterećenja, veoma često se dobija bilinearna zavisnost s/Q od s (Maksimović, 1981). U području manjih sleganja, kada je s < s1, (Slika 9.22) može se uočiti druga prava transformisane hiperbole sa parametrima a1 i b1, koja ima presek sa pravom sa parametrima a i b u područja većih sleganja pri veličini sleganja s1. Pretpostavljajući da je pri sleganju s1 došlo do pune mobilizacije nosivosti omotača šipa, odnosno nelinearno elastično – savršeno plastično ponašanje kontakta tla i omotača, i da je početni deo zavisnosti sile koja deluje na bazu šipa linearna funkcija sleganja, dobija se sledeći izraz za graničnu nosivost omotača:
|
Qs,f |
= |
s12 b1 |
(9.101) |
|
(a1 + b1s1)2 |
gde je sleganje pri plastifikaciji omotača
|
s1 |
= |
a − a1 |
(9.102) |
|
b1 − b |
Granična nosivost baze šipa se sada može odrediti kao razlika ukupne sile prema (9.100) i komponente omotača (9.101), jer je
|
Qb,f |
= |
Qf − Qs,f |
(9.103) |
DOPUŠTENO OPTEREĆENJE ŠIPA. Ako se ima u vidu da je u opštem slučaju, veličina dopuštenog sleganja merodavna za izbor dopuštenog opterećenja, za datu veličinu sleganja neće u istoj meri biti mobilisane obe komponente nosivosti šipa. Ovo je samo jedan od razloga da se faktori sigurnosti mogu definisani na više načina.
Jedan način, koji je predviđen "Pravilnikom" podrazumeva primenu "mobilisanih" parametara čvrstoće preko parcijalnih faktora sigurnosti po parametrima smičuče čvrstoće, u skladu sa ranije opisanom metodom za određivanje nosivosti plitkih temelja.
Drugi, tradicionalan način, koji je verovatno zbog svoje jednostavnosti veoma rasprostranjen u praksi, primenjuje faktor sigurnosti na graničnu silu, tako da je dopušteno korisno opterećenje šipa težine W:
|
Qa |
= |
Qf |
– |
W |
(9.104) |
|
FS |
gde je faktor sigurnosti FS = 1,8 do 4,0, sa karakterističnom vrednošću od oko 2,5.
Najčešće se zahteva FS > 3, ukoliko su granične nosivosti samo teorijski izračunate na osnovu geomehaničkih parametara a nisu proverene probnim opterećenjem (Burland 1973), tako daje dopušteno opterećenje određeno redukovanim zbirom komponenti:
|
Qa |
= |
Qs,f + Qb,f |
– |
W |
(9.105) |
|
FS |
Međutim, ako se ima u vidu mehanizam raspodele komponenti u zavisnosti od sleganja šipa prikazan na Slici 9.15, ima razloga da se manji faktor sigurnosti koristi za komponentu nosivosti omotača šipa Qs,f, jer će se ona mobilisati u znatnoj meri i pri malim sleganjima, dok se na nosivost baze, za čiji pun razvoj je potrebno znatno veće sleganje, mora manje računati, odnosno upotrebiti veći faktor sigurnosti. Obično se usvaja da je faktor sigurnosti za bazu FS,b=3 do 4, a za omotač FS,s=1,0 do 1,5, iako su moguće i druge vrednosti ukoliko se obrazlože rezultatima ispitivanja probnim opterećenjem, tako da dopušteno opterećenje šipa ne bude veće od:
|
Qa |
= |
Qb,f |
+ |
Qs,f |
– |
W |
(9.106) |
|
FS,b |
FS,s |
Jedno od praktičnih pravila za dopušteno opterećenje šipa usvaja manju vrednost od dve izračunate i to prema izrazu (9.105) za FS=2,5 i prema izrazu (9.106) za FS,s=1,0 do 1,5 i FS,b=3 do 4.
Izbor faktora sigurnosti, između ostalog, zavisi od pouzdanosti prognozirane nosivosti šipova i od dopuštenih sleganja temelja na šipovima. Podrazumeva se da, ukoliko su vršena probna opterećenja, faktori sigurnosti mogu biti u području donje granice, a ukoliko su nosivosti šipa izračunate na osnovu podataka o tlu, zavisno od pouzdanosti parametara i iskustva na istom terenu, u području srednjih ili maksimalnih vrednosti. Problematika nosivosti šipova je najčešće regulisana normativima.
NEGATIVNO TRENJE. Poseban oblik vertikalnog opterećenja šipa može nastati ukoliko se tlo u području šipa sleže u odnosu na šip u procesu konsolidacije (Slika 9.23). Dovoljna su i sasvim mala sleganja tla da izazovu dopunsko vertikalno opterećenje šipa. Pri tome u gornjem delu šipa, a često i u intervalu koji zahvata veći deo njegove ukupne dužine, smičući naponi po omotaču menjaju znak tako da se povećava opterećenje na bazu šipa, uz pojavu uvećanog sleganja. Ova pojava se naziva "negativnim trenjem" i nastaje, između ostalog, usled razlike krutosti šipa i tla. Zbog toga je pojava negativnog trenja u gornjem delu šipa češće pravilo nego izuzetak. Veličina negativnog trenja se može izračunati po postupku opisanom za pozitivno trenje, pri čemu se primenjuje β koeficijent u glinama i prašinama između 0,2 i 0,35, a u peskovima između 0,35 i 0,50. Negativno trenje se može smanjiti primenom bitumenskog premaza debljine 1-2 mm na delu stabla gotovog šipova kada se koristi β=0,05.
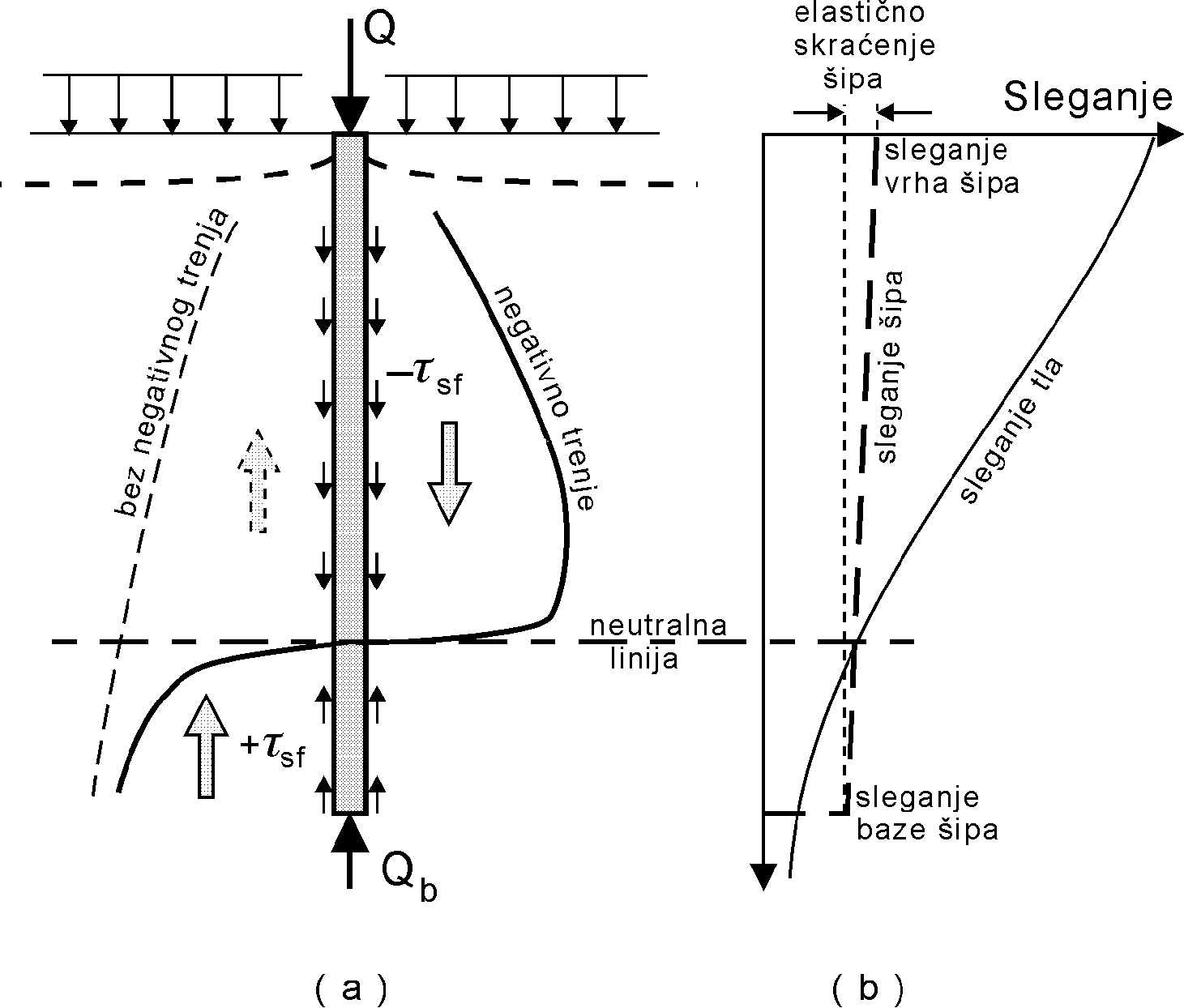
Slika 9.23. Negativno trenje – naponi smicanja i sleganja po dužini šipa
Treba imati u vidu da se negativno trenje i pozitivni otpor na kontaktu omotača šipa i tla ne mogu istovremeno pojaviti na istom delu šipa. Ako se na vrh šipa, koji je opterećen negativnim trenjem, nanese neko privremeno ili pokretno opterećenje, elastične deformacije šipa su dovoljne da mobilišu pozitivno trenje, smanjujući na taj način ukupan uticaj negativnog trenja. Kada se pokretno opterećenje ukloni, ponovo se pojavi negativno trenje jer je elastična deformacija šipa pri rasterećenju, uz odgovarajuće pomeranje naviše rasterećenog dela stabla šipa dovoljno da promeni smer napona smicanja po stablu šipa. To znači da se negativno trenje i priraštaj smičućih napona usled pokretnog opterećenja ne superponiraju, tako da se posebno provode analize za oba slučaja.
Postoji nekoliko metoda koje po navedenim principima ovaj problem rešavaju. Teorijska rešenja su, između ostalih, dali Poulos i Davis 1980 i Fellenius 1991. Prvi korak u iterativnoj analizi uticaja negativnog trenja je da se odredi položaj neutralne linije ili, preciznije rečeno, neutralne ravni, koja se nalazi na nivou gde se menjaju znaci smičućih napona na omotaču stabla šipa. Njen položaj se nalazi iz uslova da je zbir stalnog opterećenja i negativnog trenja jednak zbiru pozitivnog trenja i reakcije baze šipa. Od položaja neutralne ravni zavisi veličina maksimalne normalne sile, odnosno normalnih napona u preseku šipa, koji, u nekim okolnostima, mogu biti merodavni za sigurnost šipa, ali zavisi i veličina sleganja koja je često odlučujući faktor u praksi.
Podrazumeva se da je za analizu ovakvog zadatka potrebno raspolagati pouzdanim podacima o tlu uz pažljiv izbor računskih parametara, pri čemu treba imati u vidu da se izborom gornje granice parametara čvrstoće dobija sigurnije rešenje, što nije čest slučaj u drugim okolnostima.
S obzirom da šip ne može da se slegne više od okolnog tla, problem negativnog trenja je češće problem sleganja i napona u preseku šipa, a znatno ređe je to problem granične nosivosti tla u kome je šip ugrađen. Korisno dopušteno vertikalno opterećenje šipa sa umanjenjem za veličinu uticaja rezultante negativnog trenja Qnf je
|
Qa |
= |
Qs,f + Qb,f – 1,5Qnf |
– |
W |
(9.105) |
|
FS |
Faktor 1,5 uz Qnf je ovde uslovno uveden da se pokrije relativna nepouzdanost izračunate sile negativnog trenja i zbog činjenice da je nosivost baze šipa umanjena zbog redukcije vertikalnog efektivnog napona na nivou baze šipa usled pojave vertikalnih smičućih napona negativnog trenja.
GRUPA ŠIPOVA. Ovde su razmatrani samo neki osnovni aspekti ponašanja pojedinačnog šipa sa tačke gledišta mehanike tla. Šipovi se najčešće koriste u grupama od po nekoliko šipova ispod pojedinačne stope, do velikog broja ispod celog objekta. Tačnije određivanje raspodele sila koje deluju na pojedinačne šipove, kao i raspodela napona koji na svaki pojedinačni šip deluju u takvim okolnostima, predstavlja složen problem interakcije tla, šipova i objekta. Za šipove u grupi se obično usvaja da je nosivost grupe jednaka zbiru nosivosti pojedinačnih šipova u grupi. Međutim, grupa šipova u krupnozrnom tlu ima obično veću nosivost od zbira nosivosti pojedinačnih šipova, tako da se u takvom slučaju govori o efikasnosti grupe šipova koja je veća od jedinice. Za šipove u glini to ne mora biti slučaj, tako da se nosivost grupe proverava kao nosivost ekvivalentnog bloka, fiktivnog temelja, koji obuhvata zapreminu grupe šipova, pri čemu se obično zaključuje da je nosivost grupe praktično bliska ili jednaka zbiru nosivosti pojedinačnih šipova kada se primenjuju odgovarajuća međusobna osovinska rastojanja. Iskustva pokazuju da ako je osovinsko rastojanje šipova veće od oko 7 prečnika, svaki šip se ponaša kao pojedinačan šip. Obično se zahteva i da međusobno rastojanje šipova ne bude manje od 2,5 prečnika + 2% dužine šipa, što se u praksi često zaokružuje na 3 prečnika šipa.

Teorijska analiza sleganja pojedinačnog šipa primenom elastičnih rešenja, koja se obično zasnivaju na Midlinovom rešenju za silu u elastičnom prostoru brojna su i makako bila elegantna, ne mogu da obuhvate niz faktora koji karakterišu ponašanje stvarnog šipa u realnom tlu. Smatra se da su rešenja zasnovana na elastičnom ponašanju šipa i elastičnom tlu toliko pogrešna da nemaju nikakvu upotrebnu vrednost. Zbog toga se sa više uspeha koriste poluempirijske metode koje teorijske rezultate koriguju empirijskim faktorima. Izlaganje takvih rešenja pre spada u područje fundiranja nego mehanike tla, tako da se ovde neće prikazati. U nedostatku probnih opterećenja ili iskustava sa konkretnom vrstom šipa u datom tlu, jedno od jednostavnijih empirijskih pravila za grubu procenu veličine sleganja pojedinačnog šipa pri normalnom radnom opterećenju kaže da je sleganje vrha šipa jednako zbiru skraćenja šipa kao elastičnog štapa opterećenog silom Q na krajevima, + 1% prečnika šipa (Vesić 1970, 1975).
Od praktičnog je značaja veličina sleganja grupe šipova koja je uvek veća od sleganja pojedinačnog šipa pri istom prosečnom opterećenju šipova u grupi. Sleganje grupe šipova se može proceniti proračunom sleganja grupe kao ekvivalentnog plitkog ili poludubokog temelja, pri čemu se dubina ekvivalentnog temelja obično usvaja na donjoj trećini dužine šipova ako se veći deo opterećenja prenosi preko stabla tzv. "lebdećih" šipova, ili u nivou baza šipova ako se radi o "stojećim" šipovima. Raspodela priraštaja napona se može odrediti iz uprošćenog rešenja raspodele napona pod uglom prikazanog u Poglavlju 8, ili drugih rešenja koja se koriste za plitke temelje. Tačnost izračunatih ukupnih i relativnih sleganja grupe šipova je manja od tačnosti koja se obično postiže proračunima sleganja plitkih temelja.






























 ;
;